Thomas Young (1773-1829) – ‘The last man who knew everything’
This month’s Book of the Month by Edward Maunder is inspired by two books in our Early Science collection – Thomas Young’s A course of lectures on natural philosophy and the mechanical arts (1807) and George Peacock’s Miscellaneous works of the late Thomas Young (1855).

Thomas Young was born in Milverton, Somerset, in 1773, the eldest of ten children in a Quaker family. Soon after his birth, he was brought up by his mother’s father, Robert Davis, in Minehead, about 15 miles from Milverton.
As a young boy, Young did not find school very stimulating. He attended the village school from around four years of age and before the age of six was sent to a clergyman, ‘who had neither talent nor temper to teach anything well’. He then spent 18 months attending a boarding school near Bristol, but mostly he worked on his own, getting through the set books in less than half the time taken by the teacher.
 In 1782 he entered a school in Crompton, Dorset, which was more suitable for a young genius since pupils were given freedom to progress at their own pace. For Young, this pace was very fast, for he was undoubtedly an infant prodigy. By the time he left this school in 1786 he was knowledgeable in many languages, including ancient Greek, Latin, and Hebrew, as well as French and Italian. He had also acquired a good grounding in Newtonian physics, studied optics, and made several instruments with the help of a tutor at the school. His passion for eastern languages continued after he left the school, and he began to study Arabic, Persian, Chaldee, Syriac, and Samarian.
In 1782 he entered a school in Crompton, Dorset, which was more suitable for a young genius since pupils were given freedom to progress at their own pace. For Young, this pace was very fast, for he was undoubtedly an infant prodigy. By the time he left this school in 1786 he was knowledgeable in many languages, including ancient Greek, Latin, and Hebrew, as well as French and Italian. He had also acquired a good grounding in Newtonian physics, studied optics, and made several instruments with the help of a tutor at the school. His passion for eastern languages continued after he left the school, and he began to study Arabic, Persian, Chaldee, Syriac, and Samarian.
Although only 13 years old, Young became a tutor for the next five years. He took the opportunity to educate himself in mathematics, reading Euclid’s Elements and the works of Sir Isaac Newton. He also read other scientific works, as well as books on history and languages. In the autumn of 1792, he moved to London to begin his studies of medicine. As well as attending lectures at the Hunterian school, he enrolled as a pupil at St Bartholomew’s Hospital. Required to dissect an ox’s eye, he began to develop a theory of accommodation for the eye. He published his theories in Observations on vision, read to the Royal Society of London on 30 May 1793. Young was elected a fellow of the Royal Society on 19 June 1794.
 Young continued his medical training at the University of Edinburgh in 1794. As a Quaker he could not study at Oxford or Cambridge, so within Britain he could only obtain a degree from a Scottish university. He left Edinburgh after one year of study, but later learnt of a change in regulations by the College of Physicians requiring a period of two years study at the same university before qualifying to practise medicine. He therefore went to Emmanuel College Cambridge, but before doing so he had to declare himself a member of the Church of England. (Evidently, he did not find this hard for he had been moving steadily away from the strict Quaker rules, attending dances and the theatre while in Edinburgh.)
Young continued his medical training at the University of Edinburgh in 1794. As a Quaker he could not study at Oxford or Cambridge, so within Britain he could only obtain a degree from a Scottish university. He left Edinburgh after one year of study, but later learnt of a change in regulations by the College of Physicians requiring a period of two years study at the same university before qualifying to practise medicine. He therefore went to Emmanuel College Cambridge, but before doing so he had to declare himself a member of the Church of England. (Evidently, he did not find this hard for he had been moving steadily away from the strict Quaker rules, attending dances and the theatre while in Edinburgh.)
Although enrolled in the medical course, Young did not study medicine at Cambridge, feeling that he already knew sufficient of that subject. Rather, he worked on his own, learning more physics in order that he might pursue other interests. He had little respect for the Cambridge mathematicians:
I am ashamed to find how much the foreign mathematicians for these forty years have surpassed the English in the higher branches of the sciences.
The Cambridge men thought little of Young in return. One tutor wrote:
He seldom gave an opinion, and never volunteered one. He never laid down the law like other learned doctors, or uttered … sayings to be remembered. Indeed, like most mathematicians … he never seemed to think abstractly. A philosophical fact, a difficult calculation, an ingenious instrument, or a new invention, would engage his attention …

Royal Institution lectures
In 1801, at the age of 28, Thomas Young was appointed Professor of Natural Philosophy at the Royal Institution in London and he immediately set about preparing a series of lectures which he presented between January and May 1802. When it was repeated in 1803, the course had grown to 60 lectures and covered everything from mechanics, drawing, architecture and carpentry to music, mathematics, the properties of liquids and gases, optics, heat, electricity, gravitation, and light. The work must have been immense: in March 1802 Young admitted that ‘an immediate repetition of the labour and anxiety that I have undergone for the last 12 months would at least make me an invalid for life’. Sadly, as a public lecturer, Young was not a success. A tutor from Cambridge University commented:
I remember … his taking me with him to the Royal Institution, to hear him lecture to a number of silly women and dilettanti philosophers but nothing could show less judgment than the method he adopted; for he presumed, like many other lecturers and preachers, on the knowledge and not on the ignorance of his hearers.
According to Young’s friend, Hudson Gurney,
His style was compressed and laconic; he went into the depths of science, and indeed gave more matter than it would perhaps have been possible for persons really scientific to have followed at the moment without considerable difficulty.
After the second series of lectures in 1803, Young left the Royal Institution, and in 1804 he married Eliza Maxwell. Peacock writes:
It was a marriage of mutual affection and esteem, such as he had always looked forward to as the great object of his professional and other exertions, and secured for him a home which was graced by all the refinements of good manners and a cultivated taste: it was a singularly happy marriage.
Also in 1804 Young was made foreign secretary to the Royal Society of London, a post he filled for the rest of his life.
Young set about preparing his lectures for publication, a task which took almost 4 years. The expanded and revised versions of the lectures finally appeared in 1807 in two volumes as A Course of Lectures on Natural Philosophy and the Mechanical Arts, which also included an annotated bibliography of 20,000 relevant publications. Gurney later described the published lectures as:
a mine to which everyone has since resorted, [which] contained the original hints of more things since claimed as discoveries, than can perhaps be found in a single production of any known author.
Relevance to modern structural engineering
 Two of the lectures, XIII and XIV, are still of note for structural engineers. One concerns the material property (Young’s modulus) relating deformation to stress, and the other describes the structural actions in masonry arches. His work on arch bridges culminated in the article published in 1817 in the Encyclopaedia Britannica, and partly included in Peacock’s work of 1855.
Two of the lectures, XIII and XIV, are still of note for structural engineers. One concerns the material property (Young’s modulus) relating deformation to stress, and the other describes the structural actions in masonry arches. His work on arch bridges culminated in the article published in 1817 in the Encyclopaedia Britannica, and partly included in Peacock’s work of 1855.
In volume II of his Course of Lectures, Young defines:
The modulus of the elasticity of any substance is a column of the same substance, capable of producing a pressure on its base which is to the weight causing a certain degree of compression, as the length of the substance is to the diminution of its length.
This definition appears to be written in Young’s typically opaque style and is difficult to understand in modern terms – one of the reasons for this is the absence of the concept of ‘stress’ (force per unit area). The meaning of his definition can be explained and related to the construction of tall buildings, such as modern skyscrapers. An allowance has to be made for reductions in their heights due to a (elastic) compression of the structural material, be it concrete or steel. In today’s terms the letter E is used to denote Young’s modulus, and a column of material of height H metres would exert a pressure (as in a fluid) at its base due to its weight of ρgH N/m2, where ρ denotes the mass density kg/m3 of the material, and g denotes the gravitational acceleration m/sec2. A reduction of δ metres in height occurs due to its elasticity and its weight, and this can be derived from the equation:
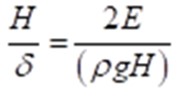 This equation supports the idea that if the reduction δ were to be equal to half the height, then E = ρgH, i.e. E is equal to the weight of a column, with cross-section of unit area and height H, that would compress by half its length.
This equation supports the idea that if the reduction δ were to be equal to half the height, then E = ρgH, i.e. E is equal to the weight of a column, with cross-section of unit area and height H, that would compress by half its length.
Young refers to experiments with ‘elastic gum’ compressed to half its length, but it would be unrealistic to experiment with steel in a similar way – nevertheless, he declares that the height of a steel column that would compress by half, is ‘nearly 1500 miles’!
Most materials behave in an elastic manner for small reductions in height, e.g.
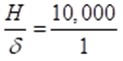
and in this case the height of a steel column equal to 510 metres, would reduce by δ equal to 51 mm due to its own weight, a relatively small but potentially significant amount of movement at the top of a skyscraper!
Edward Maunder
All references and quotes are taken from the following sources:
Kurrer, Karl-Engen, History of the Theory of Structures (2nd edition, 2018).
Santiago Huerta (editor), Essays in the history of structures (2005).
Timoshenko, Stephen, History of strength of materials (1983), p. 90-98.
Beal, Alasdair N., ‘Thomas Young and the theory of structures 1807-2007’ in The Structural Engineer, vol. 85, no. 23, (4 December 2007).
Robinson, Andrew, The Last Man Who Knew Everything (2007).
https://mathshistory.st-andrews.ac.uk/Biographies/Young_Thomas

