The celestial mechanics of Pierre-Simon Laplace (1749-1827)
As a politician, Pierre Laplace (1749-1827) had an 'incapacity for administration'; as a mathematician he was one of the greatest scientists of all time. His thinking brought him close to the origins of the universe and he was one of the first scientists to suggest the existence of what we now refer to as black holes. This guest blog is written by Edward Maunder following his rediscovery of the first four volumes of Laplace's Traité de mécanique céleste (1798-1805) in our early science collection.
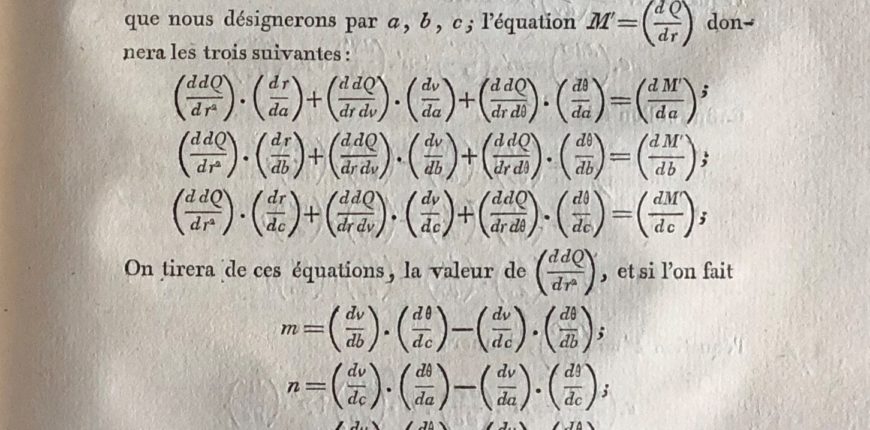
The shelves on the Outer Library Gallery include some famous scientific works. Further along from a thrilling set of complete works by Isaac Newton, I came across a set of four volumes by Pierre Laplace on celestial mechanics (regarding the motions of objects in the solar system). Traité de mécanique céleste was probably his best-known contribution to mathematics and astronomy – he also had thoughts about the origins of the universe and what are now termed black holes – and it has been thought to be as important as Newton’s contribution in the previous century. A fifth and last volume was published in 1825, not long after the Devon and Exeter Institution was founded. The first four volumes were published between 1798 and 1805, and those at the Institution are still in their original edition binding of green paper wrappers.

Laplace was born in the small village of Beaumont-en-Auge, Paye d’Auge, Calvados, in 1749 with a farming background. His father was ‘well-off in the cider trade’, and his mother came from a prosperous farming family. Despite growing up in a rural area, and resisting pressures to go into the Church, Laplace found his métier in mathematics and went to study in Paris. There, he was eventually (around the age of 30) elected to the Academie des Sciences. In 1785, he was an examiner to Napoleon Bonaparte at the Royal Artillery Corps, and in 1788 married a girl nineteen years his junior.
Laplace managed to keep his head during the French Revolution, and Napoleon promoted him to be the Minister of the Interior in 1799. He was removed from this post after six weeks, possibly ‘… because he brought the spirit of the infinitely small into the government’ or ‘because of an incapacity for administration’! As a mathematician, Laplace lived in the world of the infinitesimal governed by differential equations. Perhaps he was not best suited to government, being too meticulous and punctilious. On the other hand, other scientists criticised Laplace’s overuse of the phrase ‘it is therefore obvious that’ in his works on celestial mechanics; for one reason or another, Laplace couldn’t always be bothered to include a proof of the matter in hand – a strategy that is still very familiar to us today! Nevertheless, he received the Legion of Honour in 1805.
A dedication to Napoleon Bonaparte appears in volume 4 of Traité de mécanique céleste, dated ANXIII – 1805. The date ANXIII follows the revolutionary calendar which was finally abandoned on 22 Fructidor year XIII (9 September 1805) after some 12 years, following a report from Laplace. The Gregorian calendar was restored from 1 January 1806. After the demise of Napoleon, Laplace appears to have rethought his political ideas and allegiances, and supported the restoration of the monarchy in 1815. Laplace died at the age of 77 in 1827 with descendants issuing from his daughter, who sadly died in childbirth. His son, Emile, survived fighting for Napoleon in Russia, but had no children.

In applying mathematics to physical problems, Laplace’s approach was to:
… establish that the phenomena of nature can be reduced in the last analysis to actions at a distance between molecule and molecule, and that the consideration of these actions must serve as the basis of the mathematical theory of these phenomena.
In later years he applied his ideas to a wide range of phenomena: e.g. probability theory as applied to physical observations, capillary action, refraction of light, speed of sound, heat transfer, and the dynamics and cooling of the Earth.
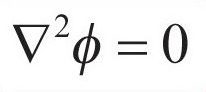
Laplace equation
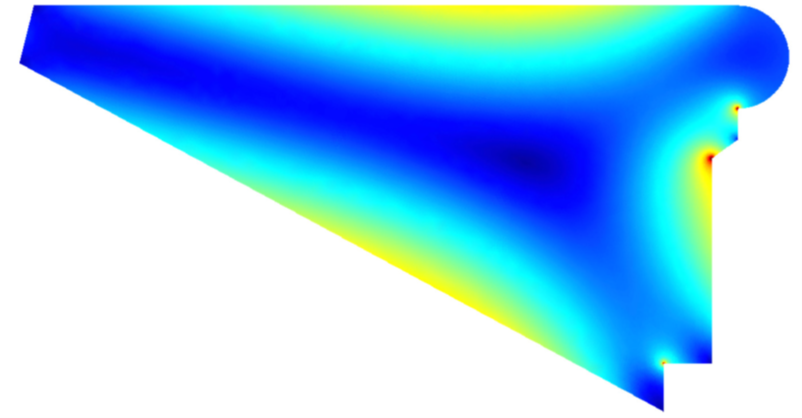
Laplace and Poisson (a former PhD student of his) are familiar to every engineering student today via equations named after them involving the so-called Laplacian operator. These equations have been applied to understanding a wide range of physical phenomena, including in recent times, the stresses that arise in a twisted shaft or beam. In today’s terminology we would say that the twisting problem requires the solution of a Poisson differential equation. Poisson was a younger colleague of Laplace and a former PhD student of his, and this is the sort of problem that they might have considered – but without today’s computers to help. The image below illustrates a cross-section through a tread of a stone staircase (popular in the 18th century). The section includes a map of shear stresses due to the twisting of a tread as the stair is loaded. This map was produced by modern methods of computational mechanics, which I’m sure would have fascinated Laplace!
Edward Maunder
I am a semi-retired structural engineer, with most of my working life having been spent in academia in Exeter, after some seven years in London working for a consulting engineering company. The nice thing about an academic life is that research interests can continue as a hobby after retirement! All I need is my laptop, skype, and I am able to collaborate with my colleagues.
I’ve been a volunteer in the DEI Library for some 19 months, and I continue to find real gems on the shelves just crying out for attention. So I have made many new friends – both in human and book forms.
References
- Mathshistory.st-andrews.ac.uk
- Laplace-beaumont-stat1.jpg-Wikimedia Commons, creator Roland Godefroy
- Chambers Biographical Dictionary, ed. Magnus Magnusson, 1990
- Private communication from Professor J. P. Moitinho de Almeida, University of Lisbon.


